スリンキーの落下

「トイ・ストーリー」に胴体がスプリングのスリンキー・ドッグが登場します。米国のおもちゃ会社が金属製のばねをスリンキーという商標で販売していたことに由来します。百均のおもちゃコーナーで樹脂製のスリンキーを入手できます。スリンキーは波の伝わり方を知るのに適したおもちゃです。

スリンキーの片端を掴んで吊るすと自重で伸びます。ばねの伸びは上側が大きく、下端に近いほど小さくなります。支える重さが減るので当然そうなるわけですが、スリンキーの各場所の変位を知りたいところです。

この状態からスリンキーを放して落下させると、面白いことに、下端の位置は上部のばねが縮むまで動かないように見えます。ほんの数分の１秒のことなので目を凝らさないと分かりにくいのですが、吊り下げたスリンキーの下端から少し離して掌で受け止めるようにして放すとよく分かります。高速度撮影したスリンキーの落下を動画でお見せします。

これはいったいどういうことでしょうか。多数の小さな重りをばねで連結したスリンキーのモデルで考えてみます。

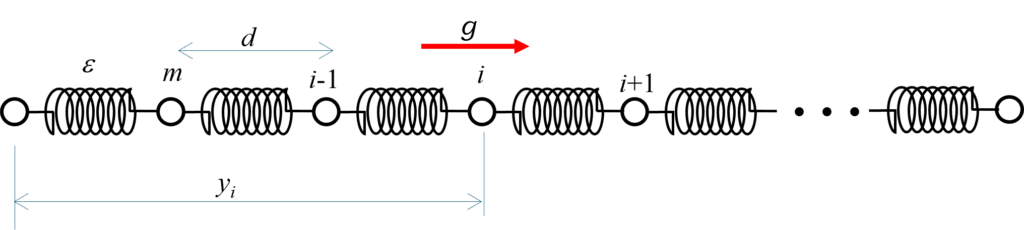
各質点の質量を \(m\)、ばねの長さを \(d\)、ばね定数を \(\varepsilon\) として、\(i\) 番目の質点の運動方程式は、吊り下げた位置を原点として位置 \(y_i\) とすると、

\[m \frac{d^2 y_i}{dt^2}=mg+\varepsilon (y_{i+1}-y_i) – \varepsilon (y_i-y_{i-1}) \]

\[m \frac{d^2 y_i}{dt^2}=mg+\varepsilon d^2 \frac{\frac{y_{i+1}-y_i}{d} – \frac{y_i-y_{i-1}}{d}}{d} \]

\(y_i\) は \(i\) 番目のスリンキー位置、すなわち \(x=id\) の部位の時刻 \(t\) における位置なので、改めて、\(y_{(x,t)}\) と書き直します。右辺の第２項は \(x\) での2階微分とみなせるので、偏微分で表すと次式に表せます。

\[\frac{m}{d} \frac{\partial^2 y}{\partial t^2}=\frac{m}{d} g+\varepsilon d \frac{\partial^2 y}{\partial x^2} \]

\[\frac{M}{L} \frac{\partial^2 y}{\partial t^2}=\frac{M}{L} g+k\frac{L}{d} d \frac{\partial^2 y}{\partial x^2} \]

\[\frac{\partial^2 y}{\partial t^2}=g+\frac{kL^2}{M} \frac{\partial^2 y}{\partial x^2} \]

\(k\) はスリンキー全体のばね定数、\(M\) は全体の質量、\(L\) は自然長でのスリンキーの長さです。モデルの小さなばねの個数を \(n\) とすると、\(k=\frac{\varepsilon}{n}\)、\(M=(n+1)m\)、\(L=nd\) です。\(n\) が十分大きければ、\(M=nm\) とみなせます。

この式は、波動方程式に重力の項が追加された形になっています。最初吊り下げられた状態では、時間変化はないので

\[0=g+\frac{kL^2}{M} \frac{\partial^2 y}{\partial x^2} \]

\(x=L\) で \( \frac{\partial y}{\partial x} =0\)、また、\(x=0\) で \(y=0\) であることを考慮して解くと、

\[y=\frac{Mg}{kL^2}(L-\frac{x}{2})x\]

ともとまります。\(x=L\) で最大となる2次関数になることが分かります。\(x=L\) での \(y\) の値が吊り下げたときのスリンキーの長さになります。その値は、

\[y_{(L,0)}=\frac{Mg}{2k}\]

となり、自重と同じ張力を加えたときの半分であることが分かります。この長さを測れば、ばね定数 \(k\) を求めることができます。\(M\) と \(L\) を別途計測します。動画のスリンキーの質量は \(38.4\ \rm g\)、自然長は \(L=65\ \rm mm\) です。吊り下げたときの長さは \(y_{(L,0)}=50\ \rm cm\) でした。これらの値からスリンキー全体のばね定数を計算すると \(k=0.38\ \rm N/m\) となります。

時間発展の \(y_{(x,t)}\) を解析的に解くのは困難なので計算機で逐次計算してみます。\(M\) と \(L\)、\(k\)を用いて計算した結果は次のようなグラフになります。\(n=200\) で計算しました。

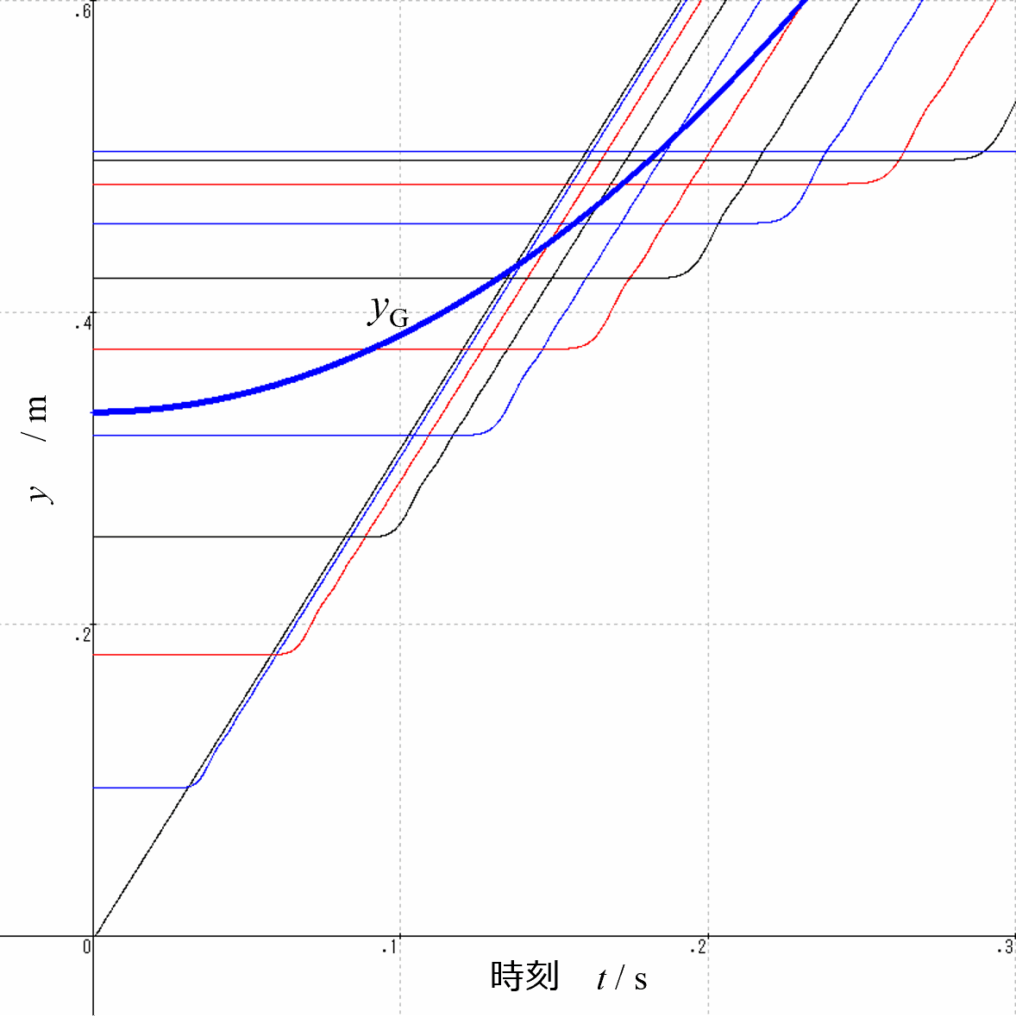
上が下を追い越すような計算結果が出るのはばね内での衝突を考慮していないためです。上の部分が落下し始めるまでその箇所は同じ場所にとどまる様子が見て取れます。ばね内での衝突がありますので、実際にはもっと複雑な運動をすると思いますが、近似的には各場所はその上の部分が縮まるまで動かないようです。動画で確認される動きが再現されています。

不思議ですが各部位は落下を始めるといずれも同じような速度で落下するようです。おそらくこれは初期の短い時間に見られる現象だと思われます。最上部付近を伝搬する縦波の速度が、これらの落下速度になっていることが推測されます。最上部では張力が \(S=mg\)、線密度が \(\displaystyle\rho=\frac{m}{2y_{(L,0)}}\) となるので、縦波の速度は \(\displaystyle v=\sqrt{\frac{S}{\rho}}=0.38\ \rm m/s\) と見積もられます。この値は、グラフの傾きと一致しています。

つまり \(y\) の位置にある部位は少なくとも \(y/v\) の時刻までは上部が放されたを知ることができないので動かないということなのでしょう。実際には下部に行くほど張力が減り、線密度が増えるので縦波の伝わる速度は遅くなり、その分だけ落下し始める時刻は遅くなります。下部になるほど静止している時間が2次関数的に長くなるのはそのことを示しているのだと思われます。実際には上部が下部を追い越して落下することはあり得ないので、ばねが上から順に縮むように見えるのだと思われます。