空気中の音速

スリンキーの落下の計算に用いた重りとばねの連結モデルは、縦波の伝搬を調べるのに使えます。そこで空気中の音速をこのモデルを使って求めてみたいと思います。

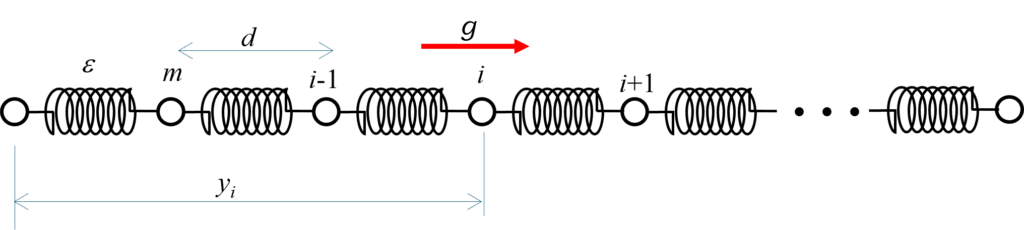
途中の計算はスリンキーの解析で用いたものと同じですが、今回は、重力を考える必要がないので、より簡単な式になります。運動方程式から重力加速度 \(g\) を取り払うと、普通の波動方程式になります。

\[ \frac{\partial^2 y}{\partial t^2}=\frac{kL^2}{M} \frac{\partial^2 y}{\partial x^2}\]

\(kL\) は単位長さのばね定数なので弾性率に対応します。空気中の音速を考えているので、体積弾性率に対応します。\(\displaystyle\frac{M}{L}\) は線密度なので、この場合は密度に対応します。

したがって、音速 \(v\) は、空気の密度を \(\rho\)、体積弾性率を \(\varepsilon\) として、\(\displaystyle v=\sqrt{\frac{\varepsilon}{\rho}}\) と表せます。

体積弾性率 \(\varepsilon\) は、

\[\varepsilon=-\frac{V}{\frac{dV}{dp}}\]

と表されます。空気は断熱性が高いので音波が伝わるときは断熱圧縮、断熱膨張により粗密波が伝搬すると考えられます。ポアソンの関係式 \[pV^{\gamma}=const.\] より

\[V=(\frac{c}{p})^{\frac{1}{\gamma}}\]

の関係が得られます。ここで \(\gamma\) は比熱比で、室温付近では空気は２原子分子の理想気体（自由度５）とみなせるので \(\displaystyle \frac{7}{5}=1.4\) です。

\[\frac{dV}{dp}=c^{\frac{1}{\gamma}}(-\frac{1}{\gamma}) p^{-\frac{1}{\gamma}-1}\]

これより、

\[\varepsilon=\gamma p\]

が得られ、音速は、状態方程式を用いて、

\[v=\sqrt{\frac{\gamma p}{\rho}}=\sqrt{\frac{\gamma RT}{M_{air}}}\]

と求まります。\(T\)は絶対温度、\(M_{air}\)は空気の分子量 \(28.8\)、\(R\) は気体定数 \(8.3\ \rm J/mol/K\) です。

温度をセ氏に換算すると、室温付近では、温度 \(t\) ℃における音速は、

\[v=331.9+0.6 t/℃ \ \rm [m/s]\]

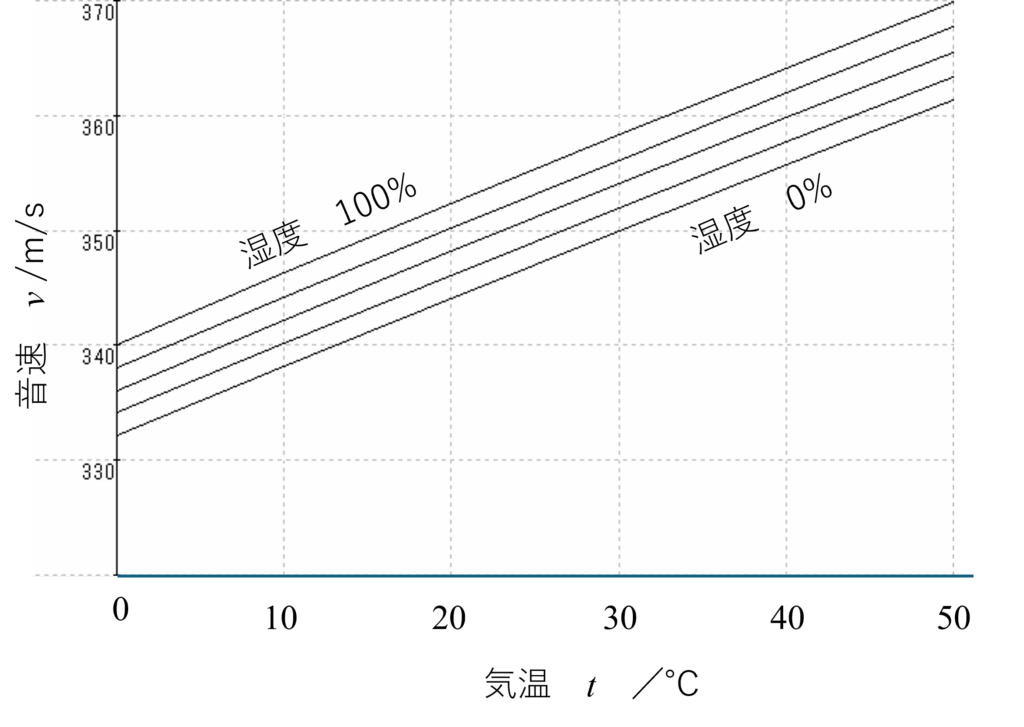
と近似できます。この解析から、\(0\)℃の音速は \(331.9\ \rm m/s\)、気温が \(1\)℃上がるにつき \(0.6\ \rm m/s\) 増えることが導けます。気体の密度が上がると音速は下がりますがこれは気体の分子量に関係するだけで気圧には無関係であることも分かります。気温が上がると音速が増すのは温度が高いと膨張して密度が下がるからではありません。勘違いしやすいので気をつけましょう。同様に気圧が下がって密度が下がっても音速に影響はありません。水素やヘリウムなど分子量の小さい気体中では音速は大きくなります。湿度が高くなると空気中の水蒸気分圧が高くなって、空気の平均分子量が小さくなります。そのため音速は増しますが、その影響は室温付近で湿度100%でも音速の増加はせいぜい2%程度です。温度変化の影響に換算すると10℃程度に対応します。気体分子の運動が粗密波のエネルギーを運んでいると解釈すれば納得できます。音速と気体分子の平均速度は比例の関係にあり、音速は気体分子の平均速度を超えることは原理的にありえないこともわかります。